[ML] 강화학습(RL)의 이해
강화학습(Reinforcement Learning)의 개념
1. 보상(Reward)과 벌칙(Publishment)
파블로프의 개, 스키너의 비둘기 실험처럼 가르칠 때, 적절한 보상과 벌을 작용하게 되면 학습의 효과가 강화된다는 것을 원리로 시작되었다.
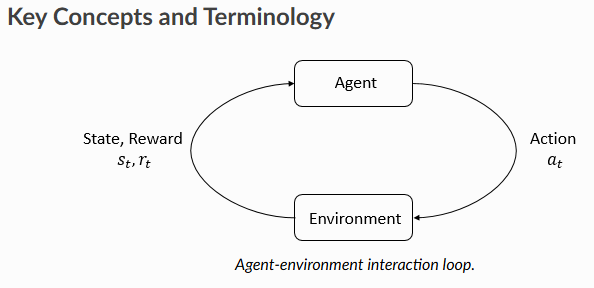
2. 시행착오: 에이전트(Agent)와 환경(Enviroment)의 상호작용
처음 게임을 시작할 때를 떠올리면 실수도 많이 하고, 낮은 점수를 획득하지만 게임을 계속하다 보면 어떤 행동이 점수를 높이는지, 어떤 행동이 게임오버로 만드는지 자연스럽게 아는 과정을 의미한다.
Agent(에이전트)는 다음과 같이 학습한다.
- 처음에는 무작위로 행동을 시도해봅니다
- 각 행동의 결과를 기억합니다
- 좋은 결과를 가져온 행동은 더 자주 시도합니다
- 나쁜 결과를 가져온 행동은 피하려고 합니다
예를 들어, 체스를 배우는 AI를 생각해 보자.
- 처음에는 말을 아무렇게나 움직입니다
- 상대방의 말을 잡으면 작은 보상을 받습니다
- 게임에서 이기면 큰 보상을 받습니다
- 점점 어떤 움직임이 승리로 이어지는지 배우게 됩니다
강화학습과 신경망
Q-learning
강화학습의 알고리즘 중 Q-learning이 있는데 상태들과 상태들마다 가능한 행동들이 저장되어 있는 Q-table을 구현하여 학습을 진행한다.
예를 들어, 미로 찾기 게임이 있다고 하자.
시작 단계:
- 처음에는 모든 행동의 가치를 0으로 시작
- 출발점에서 목적지까지 무작위로 움직이며 탐험
- 목적지에 도착하면 큰 보상(예: +100점)을 받음
- 벽에 부딪히면 작은 벌점(예: -1점)을 받음
학습 과정:
- 현재 위치 확인
- "내가 지금 어디 있지?"
- 행동 선택
- "상,하,좌,우 중에서 뭘 선택하지?"
- 처음에는 무작위로 선택
- 나중에는 Q-Table에서 가장 높은 값을 가진 방향 선택
- 결과 관찰
- "이 행동으로 어디로 이동했지?"
- "보상은 얼마를 받았지?"
- Q-Table 업데이트
- "이 행동이 좋았나? 나빴나?"
- 좋은 결과 → 해당 행동의 가치 증가
- 나쁜 결과 → 해당 행동의 가치 감소
그런데 만약 체스 게임이라고 가정하면, 아니 바둑 게임이라 가정하면?
- 체스: 1.2×10^45바이트
- 바둑: 1.39×10^175바이트
우주의 원자개수가 10^82개인데? 한계가 명확하다. 메모리를 너무 많이 차지한다.
현실적 한계:
- 현재 세계 최대 데이터 센터 저장용량: 수엑사바이트(10^18바이트) 수준
- 체스와 바둑 모두 Q-Table로는 불가능한 크기
함수근사(Function Approximation)
위와 같은 한계를 해결하기 위해 여러 노력을 기울였는데 역전파법이 등장하며 신경망(Neural Network)이 다시 한 번 떠오르게 되며 신경망으로 다차원의 비선형 함수를 근사할 수 있어 Q-table를 신경망으로 대체하는 연구가 이루어졌지만, 풀고자 하는 문제가 커질수록 신경망의 약점인 경사소실(vanishing gradient) 문제가 생겨 한계에 직면했다.
지금의 딥시크(deepseek) 처럼 알파고(alphago)의 등장으로 학습에 강화학습과 딥러닝을 적절하게 사용하고, CNN을 이용하여 패턴을 인식하고, 자가학습 과정을 통해 성능을 향상시켰다.

바둑의 상태 수 계산만 해도 우주의 원자 수보다 훨씬 큰 수였지만, 신경망을 이용해 이를 효율적으로 처리할 수 있게 되었다. 이는 단순히 바둑 AI의 발전을 넘어, 복잡한 문제를 해결하는 새로운 패러다임을 제시했다. 신경망을 통한 함수 근사는 이제 강화학습의 핵심 도구가 되어, 자율주행, 로봇 제어, 게임 AI 등 다양한 분야에서 혁신을 이끌고 있다. 이러한 발전은 앞으로 더 복잡한 현실 세계의 문제들을 해결할 수 있는 가능성을 보여주고 있다.