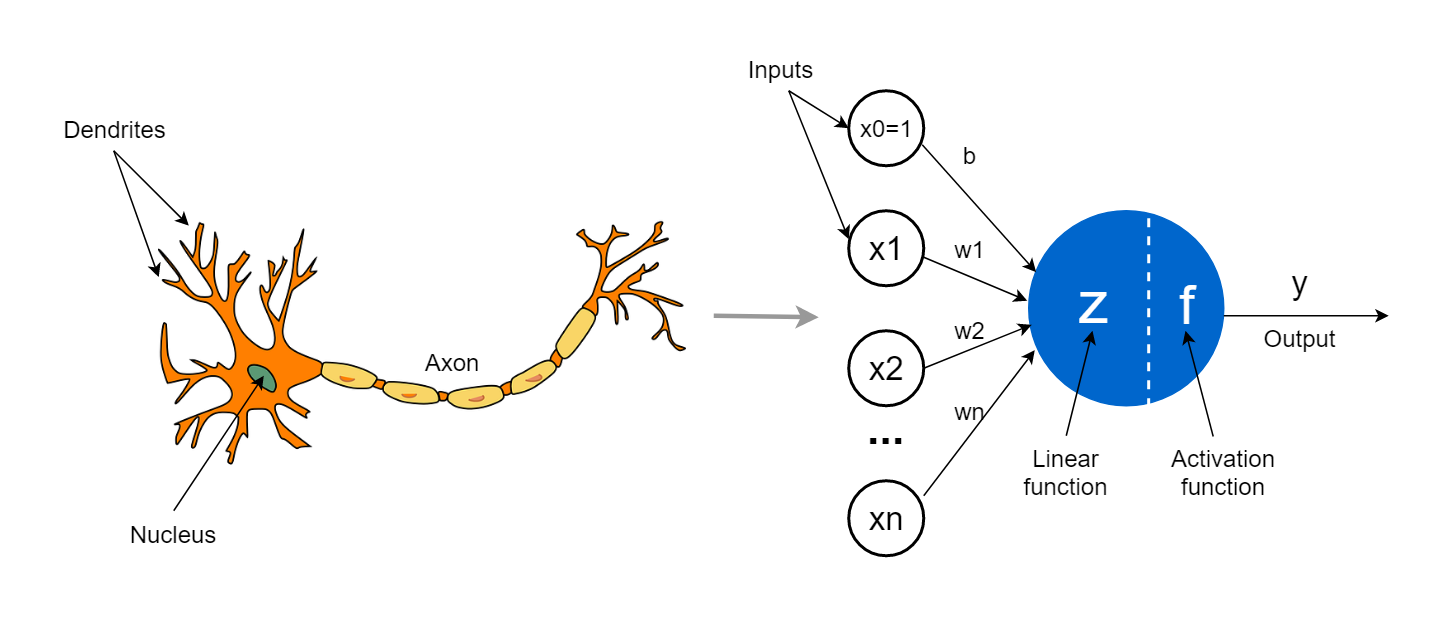
퍼셉트론(Perceptron)
- 사람의 뉴런을 표현한 수학적 모델
- 여러 개의 입력을 받아 하나의 출력을 생성
| 퍼셉트론 요소 | 생물학적 뉴런 대응 요소 | 설명 |
|---|---|---|
| 입력 값 (x_i) | 시냅스를 통한 입력 신호 | 뉴런은 여러 개의 시냅스를 통해 신호를 받음 |
| 가중치 (w_i) | 시냅스 강도 (연결 가중치) | 신호의 중요도를 조절 |
| 가중합 (z) | 수상돌기를 통한 신호의 집계 | 여러 신호를 합산하여 전달 |
| 활성화 함수 | 뉴런의 임계값 처리 | 특정 임계값을 넘으면 신호를 전달 |
| 출력 (y) | 축삭돌기를 통한 신호 전달 | 다음 뉴런으로 신호를 전달 |
Dendrite (수상돌기) - 입력을 담당
Axon(축삭돌기) - 출력을 담당
Synapse(시냅스) : 뉴런과 뉴런이 연결되는 작은 공간
- 시냅스가 가지고 있는 임계값보다 전기 신호가 크다면 시냅스가 활성화

손실 함수 (Loss Function)
신경망이 학습하는 과정에서 출력값과 정답값의 차이를 측정하는 함수
평균제곱오차 (Mean Squared Error, MSE)
- 회귀 문제에서 자주 사용
- 예측값과 실제값의 차이를 제곱하여 평균을 구하는 방식
- 공식: (미분을 고려하여 보통 n=2)

교차 엔트로피 오차 (Cross-Entropy Loss)
- 분류 문제에서 자주 사용
- 예측값과 실제값의 확률 분포 차이를 계산하여 출력이 어느정도 틀렸는지 정량화
- one-hot 인코딩 방식 사용(개-고양이 -> (1,0) - (0,1)) : 각 뉴런의 출력이 확률값을 가리킴
- 예 : 입력 데이터 x(개 데이터)에 대해 뉴런 출력값 비교
- Error = -(1) x log(0.1) - (0) x log(0.9) = 2.3 -> 오차가 큼 -> 정답과 멈
- Error = -(1) x log(0.9) - (0) x log(0.1) = 0.1 -> 오차가 작음 -> 정답에 가까움
- 공식:

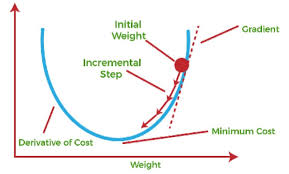
경사 하강법 (Gradient Descent)
손실 함수를 최소화하는 방향으로 가중치를 조정하는 최적화 알고리즘
- 가중치의 값을 미분한 기울기의 반대 방향으로 조금씩 움직여 손실함수 최소화
=> 델타 규칙 : Δw = η(t - y)x
주요 경사 하강법 종류(어떻게 움직일 거냐?)
- 배치 경사하강법 (Batch Gradient Descent): 전체 데이터를 사용하여 가중치를 업데이트
- 확률적 경사하강법 (Stochastic Gradient Descent, SGD): 한 개의 데이터를 사용하여 가중치를 업데이트


- 미니 배치 경사하강법 (Mini-batch Gradient Descent): 일부 데이터를 사용하여 가중치를 업데이트

에폭 (Epoch)
- 신경망이 전체 학습 데이터를 한 번 모두 학습하는 과정
- 여러 번 반복할수록 모델이 최적의 가중치를 찾을 가능성이 높아짐
신경망 학습 기법
데이터와 가중치의 관계를 근사하는 방법
선형 근사
- 단순한 직선 관계를 학습하는 방법
- 예: 선형 회귀

비선형 근사
- 비선형 관계를 학습하는 방법
- 예: 다항 회귀

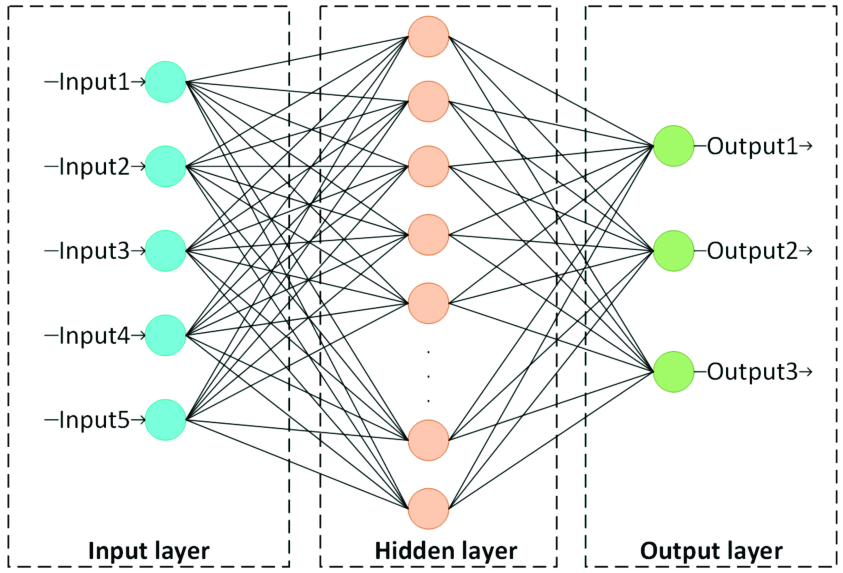
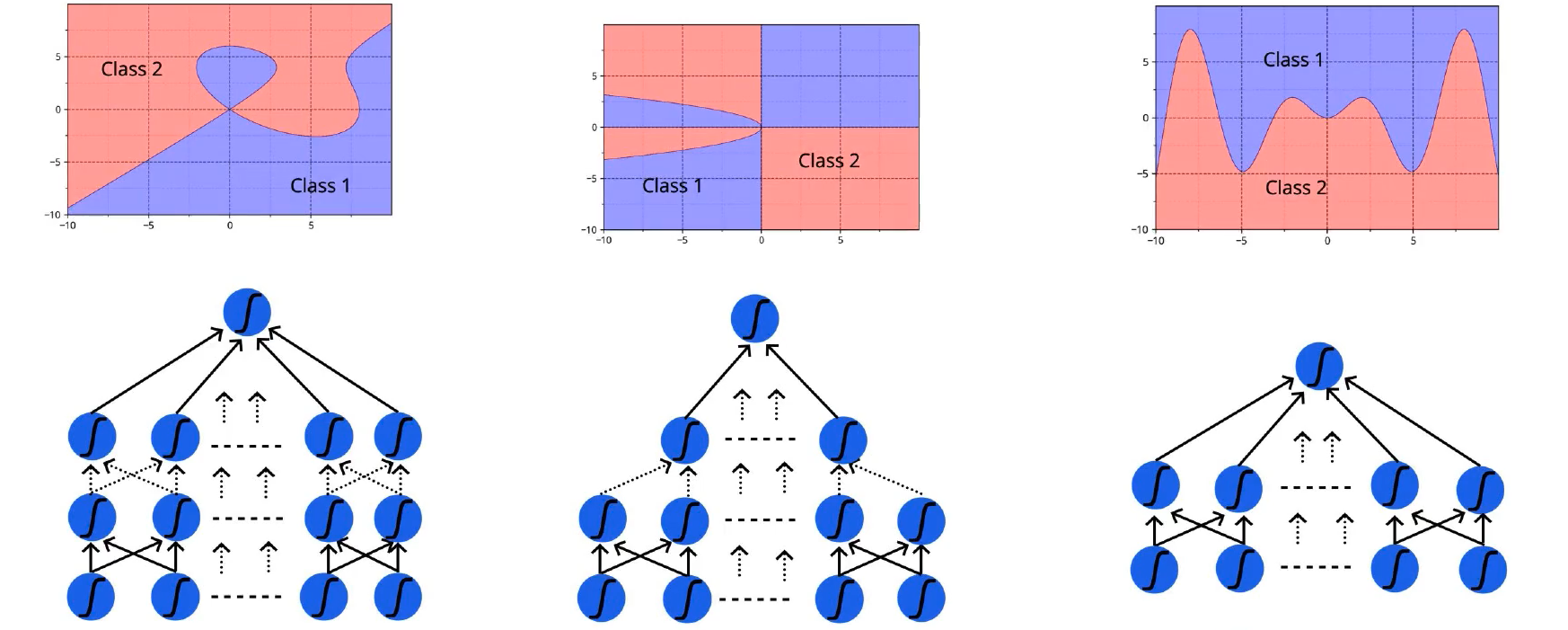
다층 퍼셉트론 (MLP, Multi-Layer Perceptron)
- 여러 개의 은닉층을 가진 신경망(XOR 문제 해결)
- 비선형성을 학습할 수 있어 복잡한 패턴을 학습 가능
활성화 함수 (Activation Function)
활성화 함수는 입력 신호를 출력 신호로 변환하는 역할
주요 활성화 함수
- 시그모이드 (Sigmoid): 값의 범위를 (0,1)로 제한하는 함수(계산이 많음)
- 하이퍼볼릭 탄젠트 (Tanh): 값의 범위를 (-1,1)로 제한하는 함수
- ReLU (Rectified Linear Unit): 음수 입력을 0으로 변환하고, 양수 입력은 그대로 유지
- 소프트맥스 (Softmax): 다중 클래스 분류 문제에서 확률 분포를 계산할 때 사용

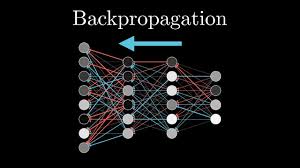
오차 역전파 (Backpropagation)
델타규칙을 다층 퍼셉트론에 적용하여 오류를 역방향으로 전파하여 신경망을 학습시키는 알고리즘
- 신경망 출력 계산
- 손실 함수 계산 → 오차 확인
- 역전파 (Backward Propagation) → 각 가중치에 대한 편향과 기여도를 편미분을 이용해 계산
- 가중치 업데이트 → 경사 하강법을 사용하여 최적화
학습 최적화(Optimizer)
더 빠르고 안정적인 학습을 위해 다양한 최적화 기법
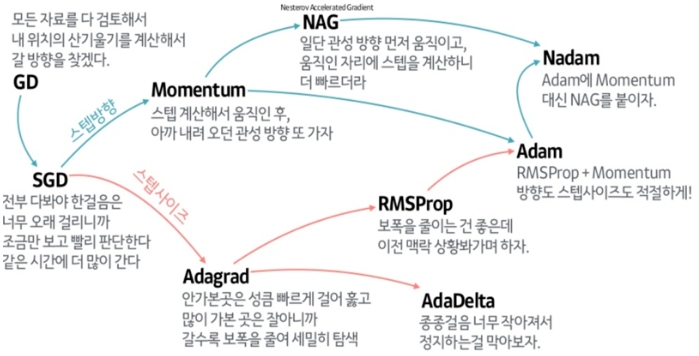
주요 최적화 기법
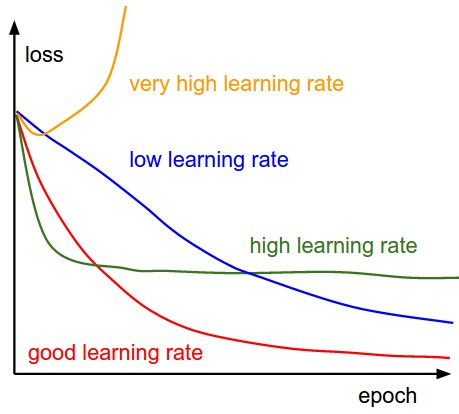
- 일정 비율 감소 (Learning Rate Decay): 학습 속도를 점진적으로 감소
- 모멘텀 (Momentum): 이전 기울기의 영향을 유지하여 더 빠른 수렴 유도
- AdaGrad: 각 가중치에 맞게 학습률을 조정하는 방법
- RMSProp: AdaGrad의 문제점을 개선하여 학습률을 조정하는 방법
- Adam (Adaptive Moment Estimation): 모멘텀과 RMSProp을 결합한 최적화 알고리즘

- 드롭아웃 (Dropout): 일부 뉴런을 무작위로 제외하여 과적합 방지

- 배치 정규화 (Batch Normalization): 입력 값을 정규화하여 학습 속도 향상
- He 초기화 (He Initialization): 가중치 초기화를 최적화하여 학습 안정화
'AI > DeepLearning' 카테고리의 다른 글
| [DL] RNN(순환신경망) 맛보기 (0) | 2025.02.18 |
|---|---|
| [DL] CNN(합성곱신경망) 맛보기 (0) | 2025.02.12 |

